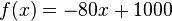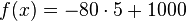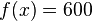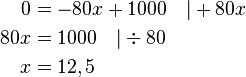Lineares Wachstum

Beim linearen Wachstum ist die Änderungsrate konstant.

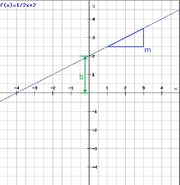
Bei der Funktion eines linearen Wachstums sind zwei Eigenschaften veränderbar, und zwar die Änderungsrate 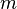${m}$ und der y-Achsenabschnitt ${b}$.
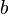Die Änderungsrate 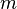${m}$ gibt an, wie stark der Bestand pro Schritt auf der x-Achse zunimmt.
Der y-Achsenabschnitt 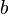${b}$ gibt an, wo der Graph der Funktion die y-Achse schneidet.

Die allgemeine Form lautet:

${f(x)={\color{Blue}m}x+{\color{OliveGreen}b}}$

Beispiel:

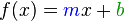
Ein kleines Kind hat in seinem Sparschwein 2€. Jeden Tag würft er weitere 50 ct in das Sparschwein. Die Geldmenge an jedem Tag nach Beobachtungsbeginn kann durch folgende Wachsttumsgleichung beschrieben werden (x in Tagen).
${m=\frac{1}{2}}$
${b=2}$
${f(x)=\frac{1}{2}x+2}$

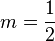
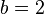
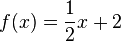
30px   Aufgabe In einer Flasche befindet sich 1 l Wasser. Die Flasche hat ein Loch, durch das gleichmäßig 80 ml pro Minute auslaufen. 1) Stellen Sie dazu eine Funktionsgleichung auf! 2) Wieviel Wasser befindet sich nach 5 Minuten noch in der Flasche? 3) Wann ist die Flasche leer?

Lösung 1) anzeigen

Lösung 1) verstecken

${f(x)=-80x+1000}$

Lösung 2) anzeigen

Lösung 2) verstecken

${f(x)=-80 \cdot 5+1000}$
${f(x)=600}$
Nach 5 Minuten befinden sich noch 600 ml in der Flasche.

Lösung 3) anzeigen

Lösung 3) verstecken

$\begin{align} 0 &=-80x+1000 \quad |+80x \\ 80x &=1000 \quad | \div 80 \\ x &=12,5 \end{align}$

Nach 12,5 Minuten ist die Flasche leer.