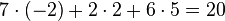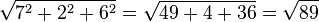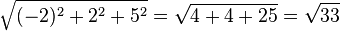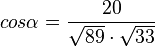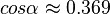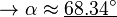Definition und Winkel zwischen Vektoren
Winkelberechnung zweier Vektoren mithilfe des Skalarprodukts
Vektoren:
allgemein:
 =
= 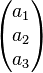
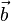 =
= 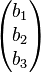
am Beispiel:
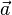 =
= 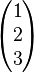
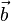 =
= 
Berechnung des Skalars:
allgemein:
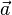

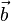 =
= 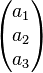

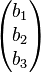 = (a1
= (a1  b1 + a2
b1 + a2  b2 + a3
b2 + a3  b3)
b3)
am Beispiel:
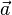

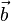 =
= 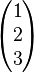

 =
= 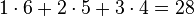
Formel zur Winkelberechnung:
Welcher Winkel wird berechnet? Welche Bedingung muss erfüllt sein, um den "richtigen" Winkel zwischen zwei Vektoren zu berechnen? [Btm]
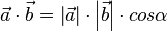
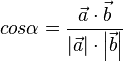 (in Formelsammlung angegeben)
(in Formelsammlung angegeben)
Errechnen von  und
und 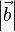 anhand des Beispiels:
anhand des Beispiels:
 =
= 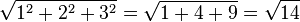
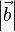 =
= 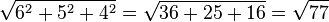
Einsetzen der Zwischenergebnisse in die Formel:
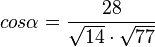
Errechnen mit Hilfe des GTRs:
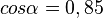
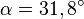
Ausnahme:
Die Ausnahme gilt, wenn das Skalarprodukt 0 ergibt. In diesem Fall weiß man, dass der Winkel zwischen den beiden Vektoren 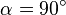 ist.
ist.
(Die weiteren Schritte müssen nicht gemacht werden!)
Beispiel:
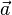 =
= 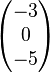
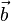 =
= 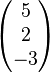
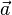

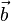 =
= 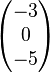

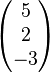 =
= 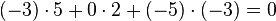
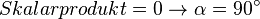
Aufgabe:
Berechne den Winkel 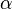 zwischen den Vektoren
zwischen den Vektoren 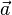 =
= 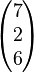 und
und 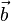 =
= 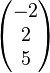
Berechnen des Skalarprodukts (für die Lösung "anzeigen" klicken)
Ausrechnen von  und
und 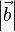 (für die Lösung "anzeigen" klicken)
(für die Lösung "anzeigen" klicken)
Einsetzen in die Formel (für die Lösung "anzeigen" klicken)
Lösung (für die Lösung "anzeigen" klicken)
von Philipp Ballmann