Die Integralfunktion
1. Was ist eine Integralfunktion?
Um verstehen zu können, was eine Integralfunktion ist, muss man wissen, was ein Integral ist und wie man eine Stammfunktion bildet.
Die Integralfunktion sieht so aus: 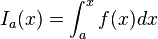
f(x) ist der Integrand und steht für die zu integrierende Gleichung.
a ist die untere
x die obere Integrationsgrenze (Grenze des Intervalls)
dx ist die Integrationsvariable
2. Wozu benötigt man die Integralfunktion/-rechnung?
1) Die Integralrechnung ermöglicht die Berechnung des Integrals von Flächen deren Begrenzungslinien Funktionen sind.
2) Berechnung von Bestand bei bekannter Änderungsrate.
3. Was ist der Unterschied zwischen Integral und Integralfunktion - Stammfunktion?
Der Unterschied zwischen einer Integralfunktion und einem Integral ist, dass man bei einer Integralfunktion,
wie der Name es schon sagt, eine Funktion erhält, bei der immer die obere Grenze eine Variable ist. Diese unbestimmte Grenze "x" wird in die Funktion eingesetzt und integriert.
Im Gegensatz zur Integralfunktion hat das bestimmte Integral zwei feste Grenzen "a" und "b".
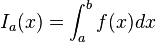
Die Integralfunktion ist genau die Stammfunktion, die F(a)=0 erfüllt.
Das Integral ist nur ein Zahlenwert. Die Integralfunktion ist somit eine Funktion, die den (orientierten) Flächeninhalt zwischen der Funktion 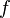 und der X-Achse zwischen der bestimmten Grenze "a" und der unbestimmten Grenze "x" angibt.
und der X-Achse zwischen der bestimmten Grenze "a" und der unbestimmten Grenze "x" angibt.
Die einzelnen Punkte der Integralfunktion setzen sich aus den Flächeninhaltswerten der möglichen rechten Grenzen zusammen.
Ein Tipp beim Bilden einer Integralfunktion ist, dass man die Funktion, die Integriert werden soll, als f(t) angibt, da die unbestimmte Grenze in der Integralfunktion bereits ein "x" enthält:
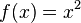
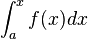
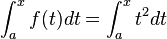
4. Wichtige Zusammnehänge zwischen f(x) f'(x) und F(x)
- f(x) ist eine gegebene Funktion
- f'(x) ist die Ableitung von f(x)
- F(x) ist die Stammfunktion von f(x)
5. Wie erhält man die Integralfunktion?
Gegeben sei eine Funktion  und eine feste untere Grenze "a"
und eine feste untere Grenze "a"
- Funktion
 integrieren (die Stammfunktion bilden)
integrieren (die Stammfunktion bilden)
Wie bilde ich eine Stammfunktion?
| f(x) (Funktion) | F(x) (Stammfunktion) |
|---|---|
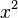 |
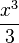 = = 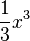
|
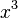 |
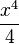 = = 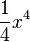
|
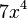 |
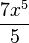 = = 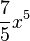
|
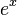 |
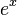
|
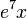 |
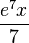
|
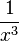 = = 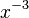 |
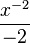 = = 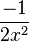
|
Gegeben ist eine Funktion f(x) = 2x
Gesucht ist die Stammfunktion d.h. wir überlegen uns, welche Funktion abgeleitet 2x ergibt.
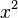 da
da 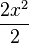 =
= 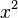
- Integral aufstellen
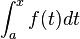
- Stammfunktion in das Integral einsetzen
- Die Grenzwerte in die Stammfunktion einsetzen
- Erhaltene Gleichungen für die Grenzen "x" und "a" voneinander subtrahieren
- Man erhält die Integralfunktion
Beispiel mit der bestimmten Grenze a=1:
1.
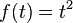
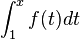
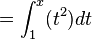
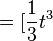
![]_1^x](/images/math/8/b/9/8b92ec87da57397e69cc07b496c32d2e.png)
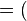
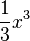
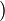 –
– 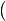
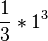
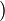
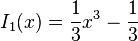
2.
 =
= 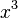
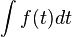 =
= 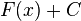
also: 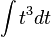 =
= 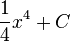
Nun sei a = 1. Wir wollen, dass 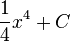 an
an 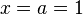 den Wert 0 annimmt, also:
den Wert 0 annimmt, also:
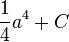 <=>
<=> 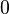 <=>
<=> 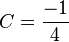
<=> 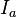 =
= 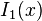 =
= 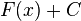 =
= 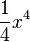 -
- 
6. Ein Beispiel für die Integralrechnung
Die Fläche unter der Funktion  =
= 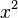 soll vom Ursprung ausgehend den Inhalt 12 Flächeneinheiten besitzen.
soll vom Ursprung ausgehend den Inhalt 12 Flächeneinheiten besitzen.
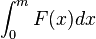 =
= 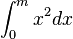
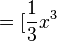
![]_0^m](/images/math/f/1/c/f1c30233fa6d301c6f977323681b2fbc.png) =
= 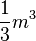 =
= 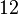
<=> 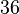 =
= 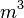 <=>
<=> 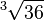 <=>
<=>