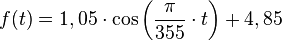Mathekurs Bittermann
Inhaltsverzeichnis |
Inhalte, Übungen und Aufgaben aus dem Kurs
Inhalte der dritten Klausur am 13.3.2012:
- Optimierungsaufgaben
- Parameterfunktionen
- Ortskurven
- Gauß-Algorithmus und seine Anwendungen (z.B. Steckbriefaufgaben)
- Ableitungen (Produkt- und Kettenregel)
Wochenaufgaben
Kürzester und längster Zaun
Her Schmidt möchte auf seinem Grundstück zum Zwecke der Tierhaltung eine rechteckige Fläche von A = 100 m2 einzäunen. Aufgrund der örtlichen Gegebenheiten kann jedoch keine Seite länger als 20 m sein.
- Wie groß muss er die Rechteckseiten a und b wählen, damit er für den Zaun möglichst wenig Material verbraucht? Wie lang ist der Zaun dann?
- Sein Sohn behauptet, wenn es einen kleinsten Umfang Umin für die Fläche gibt, gibt es auch einen größten. Ob er wohl Recht hat? Um seine Behauptung zu überprüfen, fertigt er schließlich eine grafische Darstellung der Funktion
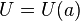 an.
an.
Lösung:
A=100m2
x<20
y<20
U=2x+2y
A=x*y=100
x=100/y
Zielfunktion:
u(y)=2*(100/y)+2y=200/y+2y
u´(y)=-200/y2+2
u´(y)=0:
-200/y2+2=0
2=200/y2 /*y2 //2
y2=100
y1=10
y2=-10 (entfällt)
Für x=y=10 ist der Umfang minimal (Quadrat).
Innige Berührung zweier Funktionen
Wenn zwei Graphen einen gemeinsamen Berührpunkt haben, dann haben diese im Berührpunkt auch die gleiche Steigung. Stimmen auch die zweiten Ableitungen überein, dann schmiegen sie sich förmlich aneinander - man sagt auch, es kommt zu einer innigen Berührung.
Dieses Verhalten soll für die Funktionen 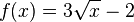 und
und 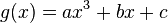 im Punkt
im Punkt 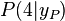 eintreten.
eintreten.
- Stellen Sie die zu überprüfenden Eigenschaften für die Funktionen f und g auf, mit denen man die "innige Berührung" mathematisch untersuchen kann.
- Ermitteln Sie die Gleichung für g(x).
- Skizzieren Sie beide Graphen in dasselbe Koordinatensystem im Intervall
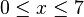 . Hinweis: Wählen Sie die Koordinatenachsen geschickt.
. Hinweis: Wählen Sie die Koordinatenachsen geschickt.
Das soll später die (versteckte) Lösung sein.
Gezeiten
An der Südküste Borkums wurden am 13. Juni 2005 bei Flut um 3.47 Uhr ein Pegelhöchststand (Hochwasser) von 5,9 m und bei der anschließenden Ebbe um 9.42 Uhr ein Pegeltiefststand (Niedrigwasser) von 3,8 m gemessen (Wasserstand bezogen auf Pegelnull).
Modellieren Sie mit einer trigonometrischen Funktion f den Pegelstand in Abhängigkeit von der Zeit. Skizzieren Sie das Schaubild von f in dem angegebenen Zeitraum.
Welche Uhrzeit liefert das Modell für den zweiten Pegelhöchststand an diesem Tag?
Am 15. Juni wurde das erste Hochwasser um 5.17 Uhr mit einem Pegelstand von 5,7 m gemessen. Vergleichen Sie mit den Vorhersagen durch das Modell und bewerten Sie Ihr Ergebnis.
Lösung:
bekannte Werte:
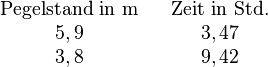
Ideen:  --> Hochpunkt;
--> Hochpunkt; 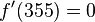 -->Tiefpunkt!
-->Tiefpunkt!
355 sind die Minuten der Differenz zwischen Ebbe und Flut (9.42 und 3.47 Uhr)
Nullpunkt festlegen: Ursprung bei Beginn der Cosinuskurve, denn weniger Variabeln auszurechnen!
Hochpunkt des Wasserstandes beginnt bei Ursprung der Cosinuskurve
zu berechnende Variabeln:
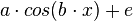
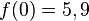
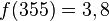
e: Pegelstand+ Differenz zwischen Hoch- und Tief-punkt --> 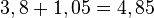
a: 1,05
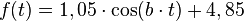
Punkt einsetzen um b auszurechnen:
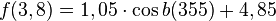
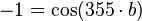
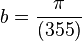
Funktion in GTR eingeben: